It’s time to reclaim the mantle of “Progress” for progressives. By falsely tethering the concept of progress to free market economics and centrist values, Steven Pinker has tried to appropriate a great idea for which he has no rightful claim.
In Enlightenment Now: The Case for Reason, Science, Humanism, and Progress, published earlier this year, Steven Pinker argues that the human race has never had it so good as a result of values he attributes to the European Enlightenment of the 18th century. He berates those who focus on what is wrong with the world’s current condition as pessimists who only help to incite regressive reactionaries. Instead, he glorifies the dominant neoliberal, technocratic approach to solving the world’s problems as the only one that has worked in the past and will continue to lead humanity on its current triumphant path.
His book has incited strong reactions, both positive and negative. On one hand, Bill Gates has, for example, effervesced that “It’s my new favorite book of all time.” On the other hand, Pinker has been fiercely excoriated by a wide range of leading thinkers for writing a simplistic, incoherent paean to the dominant world order. John Gray, in the New Statesman, calls it “embarrassing” and “feeble”; David Bell, writing in The Nation, sees it as “a dogmatic book that offers an oversimplified, excessively optimistic vision of human history”; and George Monbiot, in The Guardian, laments the “poor scholarship” and “motivated reasoning” that “insults the Enlightenment principles he claims to defend.” (Full disclosure: Monbiot recommends my book, The Patterning Instinct, instead.)
In light of all this, you might ask, what is left to add? Having read his book carefully, I believe it’s crucially important to take Pinker to task for some dangerously erroneous arguments he makes. Pinker is, after all, an intellectual darling of the most powerful echelons of global society. He spoke to the world’s elite this year at the World’s Economic Forum in Davos on the perils of what he calls “political correctness,” and has been named one of Time magazine’s “100 Most Influential People in the World Today.” Since his work offers an intellectual rationale for many in the elite to continue practices that imperil humanity, it needs to be met with a detailed and rigorous response.
Besides, I agree with much of what Pinker has to say. His book is stocked with seventy-five charts and graphs that provide incontrovertible evidence for centuries of progress on many fronts that should matter to all of us: an inexorable decline in violence of all sorts along with equally impressive increases in health, longevity, education, and human rights. It’s precisely because of the validity of much of Pinker’s narrative that the flaws in his argument are so dangerous. They’re concealed under such a smooth layer of data and eloquence that they need to be carefully unraveled. That’s why my response to Pinker is to meet him on his own turf: in each section, like him, I rest my case on hard data exemplified in a graph.
This discussion is particularly needed because progress is, in my view, one of the most important concepts of our time. I see myself, in common parlance, as a progressive. Progress is what I, and others I’m close to, care about passionately. Rather than ceding this idea to the coterie of neoliberal technocrats who constitute Pinker’s primary audience, I believe we should hold it in our steady gaze, celebrate it where it exists, understand its true causes, and most importantly, ensure that it continues in a form that future generations on this earth can enjoy. I hope this piece helps to do just that.
Graph 1: Overshoot
In November 2017, around the time when Pinker was likely putting the final touches on his manuscript, over fifteen thousand scientists from 184 countries issued a dire warning to humanity. Because of our overconsumption of the world’s resources, they declared, we are facing “widespread misery and catastrophic biodiversity loss.” They warned that time is running out: “Soon it will be too late to shift course away from our failing trajectory.”
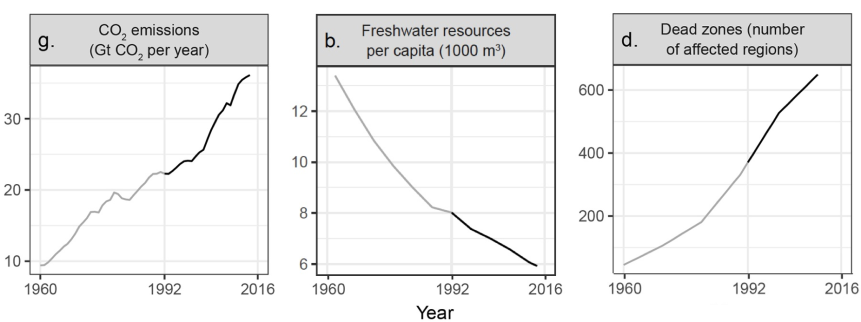
They included nine sobering charts and a carefully worded, extensively researched analysis showing that, on a multitude of fronts, the human impact on the earth’s biological systems is increasing at an unsustainable rate. Three of those alarming graphs are shown here: the rise in CO2 emissions; the decline in available freshwater; and the increase in the number of ocean dead zones from artificial fertilizer runoff.
This was not the first such notice. Twenty-five years earlier, in 1992, 1,700 scientists (including the majority of living Nobel laureates) sent a similarly worded warning to governmental leaders around the world, calling for a recognition of the earth’s fragility and a new ethic arising from the realization that “we all have but one lifeboat.” The current graphs starkly demonstrate how little the world has paid attention to this warning since 1992.
Taken together, these graphs illustrate ecological overshoot: the fact that, in the pursuit of material progress, our civilization is consuming the earth’s resources faster than they can be replenished. Overshoot is particularly dangerous because of its relatively slow feedback loops: if your checking account balance approaches zero, you know that if you keep writing checks they will bounce. In overshoot, however, it’s as though our civilization keeps taking out bigger and bigger overdrafts to replenish the account, and then we pretend these funds are income and celebrate our continuing “progress.” In the end, of course, the money runs dry and it’s game over.
Pinker claims to respect science, yet he blithely ignores fifteen thousand scientists’ desperate warning to humanity. Instead, he uses the blatant rhetorical technique of ridicule to paint those concerned about overshoot as part of a “quasi-religious ideology… laced with misanthropy, including an indifference to starvation, an indulgence in ghoulish fantasies of a depopulated planet, and Nazi-like comparisons of human beings to vermin, pathogens, and cancer.” He then uses a couple of the most extreme examples he can find to create a straw-man to buttress his caricature. There are issues worthy of debate on the topic of civilization and sustainability, but to approach a subject of such seriousness with emotion-laden rhetoric is morally inexcusable and striking evidence of Monbiot’s claim that Pinker “insults the Enlightenment principles he claims to defend.”
When Pinker does get serious on the topic, he promotes Ecomodernism as the solution: a neoliberal, technocratic belief that a combination of market-based solutions and technological fixes will magically resolve all ecological problems. This approach fails, however, to take into account the structural drivers of overshoot: a growth-based global economy reliant on ever-increasing monetization of natural resources and human activity. Without changing this structure, overshoot is inevitable. Transnational corporations, which currently constitute sixty-nine of the world’s hundred largest economies, are driven only by increasing short-term financial value for their shareholders, regardless of the long-term impact on humanity. As freshwater resources decline, for example, their incentive is to buy up what remains and sell it in plastic throwaway bottles or process it into sugary drinks, propelling billions in developing countries toward obesity through sophisticated marketing. In fact, until an imminent collapse of civilization itself, increasing ecological catastrophes are likely to enhance the GDP of developed countries even while those in less developed regions suffer dire consequences.
Graphs 2 and 3: Progress for Whom?
Which brings us to another fundamental issue in Pinker’s narrative of progress: who actually gets to enjoy it? Much of his book is devoted to graphs showing worldwide progress in quality in life for humanity as a whole. However, some of his omissions and misstatements on this topic are very telling.
At one point, Pinker explains that, “Despite the word’s root, humanism doesn’t exclude the flourishing of animals, but this book focuses on the welfare of humankind.” That’s convenient, because any non-human animal might not agree that the past sixty years has been a period of flourishing. In fact, while the world’s GDP has increased 22-fold since 1970, there has been a vast die-off of the creatures with whom we share the earth. As shown in Figure 2, human progress in material consumption has come at the cost of a 58% decline in vertebrates, including a shocking 81% reduction of animal populations in freshwater systems. For every five birds or fish that inhabited a river or lake in 1970, there is now just one.

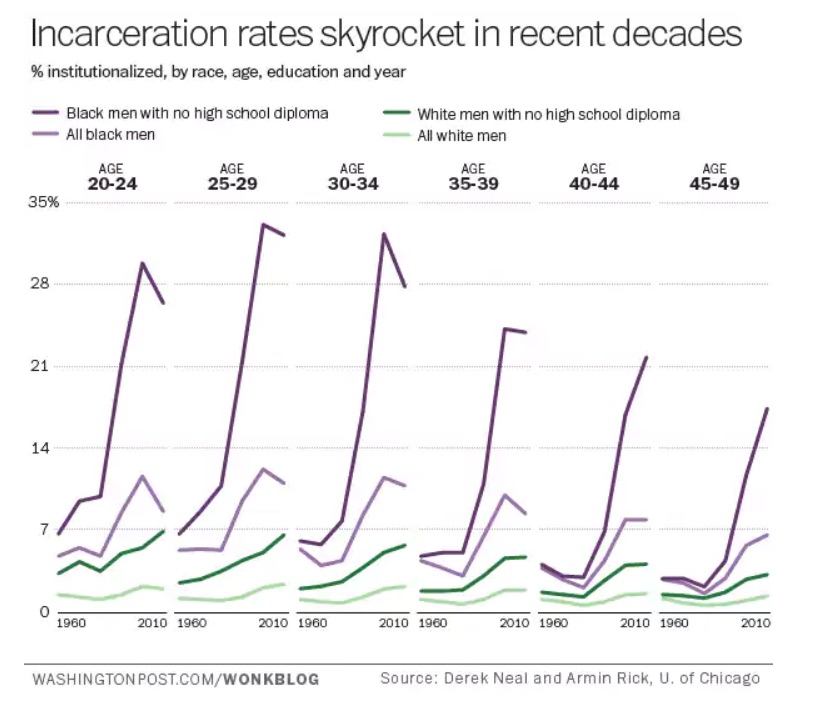
But we don’t need to look outside the human race for Pinker’s selective view of progress. He is pleased to tell us that “racist violence against African Americans… plummeted in the 20th century, and has fallen further since.” What he declines to report is the drastic increase in incarceration rates for African Americans during that same period (Figure 3). An African American man is now six times more likely to be arrested than a white man, resulting in the dismal statistic that one in every three African American men can currently expect to be imprisoned in their lifetime. The grim takeaway from this is that racist violence against African Americans has not declined at all, as Pinker suggests. Instead, it has become institutionalized into U.S. national policy in what is known as the school-to-prison pipeline.
Graph 4: A rising tide lifts all boats?
This brings us to one of the crucial errors in Pinker’s overall analysis. By failing to analyze his top-level numbers with discernment, he unquestioningly propagates one of the great neoliberal myths of the past several decades: that “a rising tide lifts all the boats”—a phrase he unashamedly appropriates for himself as he extols the benefits of inequality. This was the argument used by the original instigators of neoliberal laissez-faire economics, Ronald Reagan and Margaret Thatcher, to cut taxes, privatize industries, and slash public services with the goal of increasing economic growth.
Pinker makes two key points here. First, he argues that “income inequality is not a fundamental component of well-being,” pointing to recent research that people are comfortable with differential rewards for others depending on their effort and skill. However, as Pinker himself acknowledges, humans do have a powerful predisposition toward fairness. They want to feel that, if they work diligently, they can be as successful as someone else based on what they do, not on what family they’re born into or what their skin color happens to be. More equal societies are also healthier, which is a condition conspicuously missing from the current economic model, where the divide between rich and poor has become so gaping that the six wealthiest men in the world (including Pinker’s good friend, Bill Gates) now own as much wealth as the entire bottom half of the world’s population.
Pinker’s fallback might, then, be his second point: the rising tide argument, which he extends to the global economy. Here, he cheerfully recounts the story of how Branko Milanović, a leading ex-World Bank economist, analyzed income gains by percentile across the world over the twenty-year period 1988–2008, and discovered something that became widely known as the “Elephant Graph,” because its shape resembled the profile of an elephant with a raised trunk. Contrary to popular belief about rising global inequality, it seemed to show that, while the top 1% did in fact gain more than their fair share of income, lower percentiles of the global population had done just as well. It seemed to be only the middle classes in wealthy countries that had missed out.
This graph, however, is virtually meaningless because it calculates growth rates as a percent of widely divergent income levels. Compare a Silicon Valley executive earning $200,000/year with one of the three billion people currently living on $2.50 per day or less. If the executive gets a 10% pay hike, she can use the $20,000 to buy a new compact car for her teenage daughter. Meanwhile, that same 10% increase would add, at most, a measly 25 cents per day to each of those three billion. In Graph 4, Oxfam economist Mujeed Jamaldeen shows the original “Elephant Graph” (blue line) contrasted with changes in absolute income levels (green line). The difference is stark.

The “Elephant Graph” elegantly conceals the fact that the wealthiest 1% experienced nearly 65 times the absolute income growth as the poorest half of the world’s population. Inequality isn’t, in fact, decreasing at all, but going extremely rapidly the other way. Jamaldeen has calculated that, at the current rate, it would take over 250 years for the income of the poorest 10% to merely reach the global average income of $11/day. By that time, at the current rate of consumption by wealthy nations, it’s safe to say there would be nothing left for them to spend their lucrative earnings on. In fact, the “rising tide” for some barely equates to a drop in the bucket for billions of others.
Graph 5: Measuring Genuine Progress
One of the cornerstones of Pinker’s book is the explosive rise in income and wealth that the world has experienced in the past couple of centuries. Referring to the work of economist Angus Deaton, he calls it the “Great Escape” from the historic burdens of human suffering, and shows a chart (Figure 5, left) depicting the rise in Gross Domestic Product (GDP) per capita, which seems to say it all. How could anyone in their right mind refute that evidence of progress?
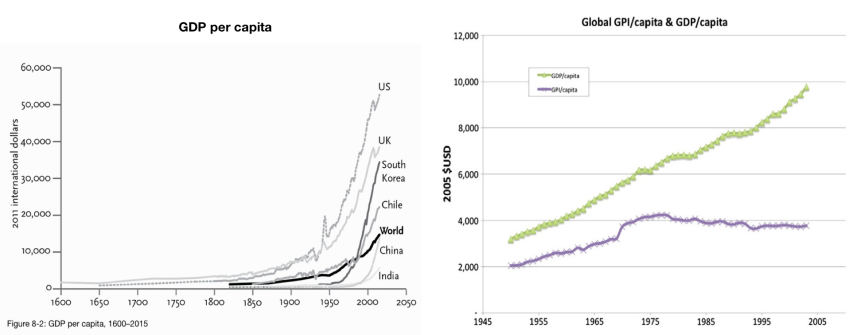
There is no doubt that the world has experienced a transformation in material wellbeing in the past two hundred years, and Pinker documents this in detail, from the increased availability of clothing, food, and transportation, to the seemingly mundane yet enormously important decrease in the cost of artificial light. However, there is a point where the rise in economic activity begins to decouple from wellbeing. In fact, GDP merely measures the rate at which a society is transforming nature and human activities into the monetary economy, regardless of the ensuing quality of life. Anything that causes economic activity of any kind, whether good or bad, adds to GDP. An oil spill, for example, increases GDP because of the cost of cleaning it up: the bigger the spill, the better it is for GDP.
This divergence is played out, tragically, across the world every day, and is cruelly hidden in global statistics of rising GDP when powerful corporate and political interests destroy the lives of the vulnerable in the name of economic “progress.” In just one of countless examples, a recent report in The Guardian describes how indigenous people living on the Xingu River in the Amazon rainforest were forced off their land to make way for the Belo Monte hydroelectric complex in Altamira, Brazil. One of them, Raimundo Brago Gomes, tells how “I didn’t need money to live happy. My whole house was nature… I had my patch of land where I planted a bit of everything, all sorts of fruit trees. I’d catch my fish, make manioc flour… I raised my three daughters, proud of what I was. I was rich.” Now, he and his family live among drug dealers behind barred windows in Brazil’s most violent city, receiving a state pension which, after covering rent and electricity, leaves him about 50 cents a day to feed himself, his wife, daughter, and grandson. Meanwhile, as a result of his family’s forced entry into the monetary economy, Brazil’s GDP has risen.
Pinker is aware of the crudeness of GDP as a measure, but uses it repeatedly throughout his book because, he claims, “it correlates with every indicator of human flourishing.” This is not, however, what has been discovered when economists have adjusted GDP to incorporate other major factors that affect human flourishing. One prominent alternative measure, the Genuine Progress Indicator (GPI), reduces GDP for negative environmental factors such as the cost of pollution, loss of primary forest and soil quality, and social factors such as the cost of crime and commuting. It increases the measure for positive factors missing from GDP such as housework, volunteer work, and higher education. Sixty years of historical GPI for many countries around the world have been measured, and the results resoundingly refute Pinker’s claim of GDP’s correlation with wellbeing. In fact, as shown by the purple line in Figure 5 (right), it turns out that the world’s Genuine Progress peaked in 1978 and has been steadily falling ever since.
Graph 6: What Has Improved Global Health?
One of Pinker’s most important themes is the undisputed improvement in overall health and longevity that the world has enjoyed in the past century. It’s a powerful and heart-warming story. Life expectancy around the world has more than doubled in the past century. Infant mortality everywhere is a tiny fraction of what it once was. Improvements in medical knowledge and hygiene have saved literally billions of lives. Pinker appropriately quotes economist Steven Radelet that these improvements “rank among the greatest achievements in human history.”
So, what has been the underlying cause of this great achievement? Pinker melds together what he sees as the twin engines of progress: GDP growth and increase in knowledge. Economic growth, for him, is a direct result of global capitalism. “Though intellectuals are apt to do a spit take when they read a defense of capitalism,” he declares with his usual exaggerated rhetoric, “its economic benefits are so obvious that they don’t need to be shown with numbers.” He refers to a figure called the Preston curve, from a paper by Samuel Preston published in 1975 showing a correlation between GDP and life expectancy that become foundational to the field of developmental economics. “Most obviously,” Pinker declares, “GDP per capita correlates with longevity, health, and nutrition.” While he pays lip service to the scientific principle that “correlation is not causation,” he then clearly asserts causation, claiming that “economic development does seem to be a major mover of human welfare.” He closes his chapter with a joke about a university dean offered by a genie the choice between money, fame, or wisdom. The dean chooses wisdom but then regrets it, muttering “I should have taken the money.”
Pinker would have done better to have pondered more deeply on the relation between correlation and causation in this profoundly important topic. In fact, a recent paper by Wolfgang Lutz and Endale Kebede entitled “Education and Health: Redrawing the Preston Curve” does just that. The original Preston curve came with an anomaly: the relationship between GDP and life expectancy doesn’t stay constant. Instead, each period it’s measured, it shifts higher, showing greater life expectancy for any given GDP (Figure 6, left). Preston—and his followers, including Pinker—explained this away by suggesting that advances in medicine and healthcare must have improved things across the board.

Lutz and Kebede, however, used sophisticated multi-level regression models to analyze how closely education correlated with life expectancy compared with GDP. They found that a country’s average level of educational attainment explained rising life expectancy much better than GDP, and eliminated the anomaly in Preston’s Curve (Figure 6, right). The correlation with GDP was spurious. In fact, their model suggests that both GDP and health are ultimately driven by the amount of schooling children receive. This finding has enormous implications for development priorities in national and global policy. For decades, the neoliberal mantra, based on Preston’s Curve, has dominated mainstream thinking—raise a country’s GDP and health benefits will follow. Lutz and Kebede show that a more effective policy would be to invest in schooling for children, with all the ensuing benefits in quality of life that will bring.
Pinker’s joke has come full circle. In reality, for the past few decades, the dean chose the money. Now, he can look at the data and mutter: “I should have taken the wisdom.”
Graph 7: False Equivalencies, False Dichotomies
As we can increasingly see, many of Pinker’s missteps arise from the fact that he conflates two different dynamics of the past few centuries: improvements in many aspects of the human experience, and the rise of neoliberal, laissez-faire capitalism. Whether this is because of faulty reasoning on his part, or a conscious strategy to obfuscate, the result is the same. Most readers will walk away from his book with the indelible impression that free market capitalism is an underlying driver of human progress.
Pinker himself states the importance of avoiding this kind of conflation. “Progress,” he declares, “consists not in accepting every change as part of an indivisible package… Progress consists of unbundling the features of a social process as much as we can to maximize the human benefits while minimizing the harms.” If only he took his own admonition more seriously!
Instead, he laces his book with an unending stream of false equivalencies and false dichotomies that lead a reader inexorably to the conclusion that progress and capitalism are part of the same package. One of his favorite tropes is to create a false equivalency between right-wing extremism and the progressive movement on the left. He tells us that the regressive factions that undergirded Donald Trump’s presidency were “abetted by a narrative shared by many of their fiercest opponents, in which the institutions of modernity have failed and every aspect of life is in deepening crisis—the two sides in macabre agreement that wrecking those institutions will make the world a better place.” He even goes so far as to implicate Bernie Sanders in the 2016 election debacle: “The left and right ends of the political spectrum,” he opines, “incensed by economic inequality for their different reasons, curled around to meet each other, and their shared cynicism about the modern economy helped elect the most radical American president in recent times.”
Implicit in Pinker’s political model is the belief that progress can only arise from the brand of centrist politics espoused by many in the mainstream Democratic Party. He perpetuates a false dichotomy of “right versus left” based on a twentieth-century version of politics that has been irrelevant for more than a generation. “The left,” he writes, “has missed the boat in its contempt for the market and its romance with Marxism.” He contrasts “industrial capitalism,” on the one hand, which has rescued humanity from universal poverty, with communism, which has “brought the world terror-famines, purges, gulags, genocides, Chernobyl, megadeath revolutionary wars, and North Korea–style poverty before collapsing everywhere else of its own internal contradictions.”
By painting this black and white, Manichean landscape of capitalist good versus communist evil, Pinker obliterates from view the complex, sophisticated models of a hopeful future that have been diligently constructed over decades by a wide range of progressive thinkers. These fresh perspectives eschew the Pinker-style false dichotomy of traditional left versus right. Instead, they explore the possibilities of replacing a destructive global economic system with one that offers potential for greater fairness, sustainability, and human flourishing. In short, a model for continued progress for the twenty-first century.
While the thought leaders of the progressive movement are too numerous to mention here, an illustration of this kind of thinking is seen in Graph 7. It shows an integrated model of the economy, aptly called “Doughnut Economics,” that has been developed by pioneering economist Kate Raworth. The inner ring, called Social Foundation, represents the minimum level of life’s essentials, such as food, water, and housing, required for the possibility of a healthy and wholesome life. The outer ring, called Ecological Ceiling, represents the boundaries of Earth’s life-giving systems, such as a stable climate and healthy oceans, within which we must remain to achieve sustained wellbeing for this and future generations. The red areas within the ring show the current shortfall in the availability of bare necessities to the world’s population; the red zones outside the ring illustrate the extent to which we have already overshot the safe boundaries in several essential earth systems. Humanity’s goal, within this model, is to develop policies that bring us within the safe and just space of the “doughnut” between the two rings.

Raworth, along with many others who care passionately about humanity’s future progress, focus their efforts, not on the kind of zero-sum, false dichotomies propagated by Pinker, but on developing fresh approaches to building a future that works for all on a sustainable and flourishing earth.
Graph 8: Progress Is Caused By… Progressives!
This brings us to the final graph, which is actually one of Pinker’s own. It shows the decline in recent years of web searches for sexist, racist, and homophobic jokes. Along with other statistics, he uses this as evidence in his argument that, contrary to what we read in the daily headlines, retrograde prejudices based on gender, race, and sexual orientation are actually on the decline. He attributes this in large part to “the benign taboos on racism, sexism, and homophobia that have become second nature to the mainstream.”

How, we might ask, did this happen? As Pinker himself expresses, we can’t assume that this kind of moral progress just happened on its own. “If you see that a pile of laundry has gone down,” he avers, “it does not mean the clothes washed themselves; it means someone washed the clothes. If a type of violence has gone down, then some change in the social, cultural, or material milieu has caused it to go down… That makes it important to find out what the causes are, so we can try to intensify them and apply them more widely.”
Looking back into history, Pinker recognizes that changes in moral norms came about because progressive minds broke out of their society’s normative frames and applied new ethics based on a higher level of morality, dragging the mainstream reluctantly in their wake, until the next generation grew up adopting a new moral baseline. “Global shaming campaigns,” he explains, “even when they start out as purely aspirational, have in the past led to dramatic reductions in slavery, dueling, whaling, foot-binding, piracy, privateering, chemical warfare, apartheid, and atmospheric nuclear testing.”
It is hard to comprehend how the same person who wrote these words can then turn around and hurl invectives against what he decries as “political correctness police, and social justice warriors” caught up in “identity politics,” not to mention his loathing for an environmental movement that “subordinates human interests to a transcendent entity, the ecosystem.” Pinker seems to view all ethical development from prehistory to the present day as “progress,” but any pressure to shift society further along its moral arc as anathema.
This is the great irony of Pinker’s book. In writing a paean to historical progress, he then takes a staunchly conservative stance to those who want to continue it. It’s as though he sees himself at the mountain’s peak, holding up a placard saying “All progress stops here, unless it’s on my terms.”
In reality, many of the great steps made in securing the moral progress Pinker applauds came from brave individuals who had to resist the opprobrium of the Steven Pinkers of their time while they devoted their lives to reducing the suffering of others. When Thomas Paine affirmed the “Rights of Man” back in 1792, he was tried and convicted in absentia by the British for seditious libel. It would be another 150 years before his visionary idea was universally recognized in the United Nations. Emily Pankhurst was arrested seven times in her struggle to obtain women’s suffrage and was constantly berated by “moderates” of the time for her radical approach in striving for something that has now become the unquestioned norm. When Rachel Carson published Silent Spring in 1962, with the first public exposé of the indiscriminate use of pesticides, her solitary stance was denounced as hysterical and unscientific. Just eight years later, twenty million Americans marched to protect the environment in the first Earth Day.
These great strides in moral progress continue to this day. It’s hard to see them in the swirl of daily events, but they’re all around us: in the legalization of same sex marriage, in the spread of the Black Lives Matter movement, and most recently in the way the #MeToo movement is beginning to shift norms in the workplace. Not surprisingly, the current steps in social progress are vehemently opposed by Steven Pinker, who has approvingly retweeted articles attacking both Black Lives Matter and #MeToo, and who rails at the World Economic Forum against what he terms “political correctness.”
It’s time to reclaim the mantle of “Progress” for progressives. By slyly tethering the concept of progress to free market economics and centrist values, Steven Pinker has tried to appropriate a great idea for which he has no rightful claim. Progress in the quality of life, for humans and nonhumans alike, is something that anyone with a heart should celebrate. It did not come about through capitalism, and in many cases, it has been achieved despite the “free market” that Pinker espouses. Personally, I’m proud to be a progressive, and along with many others, to devote my energy to achieve progress for this and future generations. And if and when we do so, it won’t be thanks to Steven Pinker and his specious arguments.
Jeremy Lent is author of The Patterning Instinct: A Cultural History of Humanity’s Search for Meaning, which investigates how different cultures have made sense of the universe and how their underlying values have changed the course of history. He is founder of the nonprofit Liology Institute, dedicated to fostering a sustainable worldview. For more information visit jeremylent.com.

Dear Jeremy,
Thanks for the comments.
Nalin
On Thu, May 17, 2018 at 11:56 PM, Patterns of Meaning wrote:
> [image: Boxbe] This message is eligible > for Automatic Cleanup! (comment-reply@wordpress.com) Add cleanup rule > > | More info > > > Jeremy posted: “It’s time to reclaim the mantle of “Progress” for > progressives. By falsely tethering the concept of progress to free market > economics and centrist values, Steven Pinker has tried to appropriate a > great idea for which he has no rightful claim. In Enlighte” >
LikeLike
I’ve come to believe that almost everything has both pros and cons and really depends not only on one’s perspective but one’s own biases and prejudices, and a very strong drive to reduce personal cognitive dissonance. Complex systems are by their very nature non-linear but humans tend to think in very linear terms. As a result, we often (if not always) misattribute causes to the world we observe–to say little about the idea that we are rationalising animals, not rational ones.
The fact that Steven Pinker “…glorifies the dominant neoliberal, technocratic approach to solving the world’s problems…” is not surprising given that he is very much a part of that worldview/paradigm. Justifying the status quo that one is a part of is quite normal. Getting someone to see the world differently when one derives a living from it is next to impossible.
One could easily argue that the ‘progress’ we have witnessed over the past couple of centuries has little to do with a shift in values attributed to the Enlightenment but far more to do with our exploitation of a particular set of energy resources (i.e. fossil fuels). And if this is indeed the case (and we truly don’t know what the future holds as the ‘experiment’ is still playing out), then all of the ‘progress’ that we have experienced is in significant jeopardy as the foundational energy that has allowed it to occur is, after all, finite.
And, of course, any species that comes to depend so meaningfully on a finite resource is staring overshoot and collapse in the face (as the article argues)–to say little about the Law of Diminishing Marginal Returns that seems to have afflicted virtually every complex society in the past and led to collapse.
Finally, one of the biggest hurdles I’ve come to better appreciate is the credit/debt-based fiat currency system that has been foisted upon the world’s citizens. This system not only pushes the culture of infinite growth upon us but demands it otherwise it would collapse as any Ponzi eventually does. As long as we use such a monetary system we seem destined to experience overshoot and collapse. It is a matter of when, not if.
LikeLiked by 2 people
Thanks Jeremy, for some provoking ideas and some good counterpoints to consider as I read Pinker’s book. I found Pinker’s reference to entropy a useful touchstone for his argument about progress – that it is not ‘set and forget’, but it needs constant attention to address the new issues that arise from (and seek inexorably to undo the good work of) solving the old ones – a mantra I suspect a progressive such as yourself would subscribe to. The shocking incarceration rates of African Americans post the civil rights movement could be seen as a kind of transformed institutional violence as you posit, but even your own graphs here suggest a ‘correcting force’ at work in about 1990(?) that would seem to suggest that this undesirable phenomena that coincided with the CRM is being addressed. Theories abound, no-one quite knows why this is happening, (see Pew Research; Washington Post on this topic) but this would seem to play into Pinker’s theory that the enlightenment has tended society in the direction of improvement in this area: ending slavery, ending Jim Crow, endowing civil rights and – now – reducing black incarceration rates. You end the article by oddly backing ‘progressives’, as the progenators of history’s progress, as though Pinker would disagree with you. I don’t think he would, but I think he would emphasise their being rational, reasoned thinkers as the cause of their progress, and not their status as “progressives”. I also think that to retrospectively label these enlightenment thinkers as progressives is one thing, but we can’t therefore assume that modern-day, self-proclaimed political progressives are their natural descendants, particularly when some on the extreme left are expressly anti-rational in their post-modernist views. But thank you for a good article that gave me lots to consider about Pinker’s book.
LikeLike
Having read not just through your article, but also observing the rhetoric and open opprobrium, I have the impression that both you and Pinker represent extremities. While I very much appreciate you taking not just a nuanced stance on many factors, but also questioning established metrics, I find it an irony that this critical aspect finds no obvious place when it comes to your own beliefs. E.g. political correctness and #metoo, where you staunchly defend them as being not just right, but also being righteous. #metoo is a power game which instrumentalises sex and gender to the detriment of human males. As for political correctness, it has indeed taken on demonic and oppressive forms. If you haven’t yet noticed it, I wonder why…
LikeLike
Agreed to most, and I did write an essay excoriating Pinker, February 5, 2018, along similar lines.
These are the most dangerous times, not just for civilization, and humanity, but even for the biosphere. Everything collapses, except for one thing: the good fortune of the plutocracy Pinker is attached to, and thrives from. So his fanatical optimism is self-serving.
It is important to free ourselves from tribalization, nationalism. The declaration of the Rights of Man and the Citizen was from the National Constituent Assembly of France, 1789. This is what the UN Charter derives from. Paine just repeated some of its elements.
LikeLike
Then again, the French Revolution was inspired by the American Revolution. And a number of people argued at the time that the American Revolution would have failed if not for Thomas Paine who inspired colonists to fight. In Common Sense (1775-1776), Paine wrote of “natural rights of all Mankind”. And in The Crisis (1776-1783), he spoke in great detail about rights, legislative rights, essential rights, natural rights, and birthright.
The Declaration of Independence also famously spoke of both legal and natural rights: “We hold these truths to be self-evident, that all men are created equal, that they are endowed by their Creator with certain unalienable Rights, that among these are Life, Liberty and the pursuit of Happiness.” Some have argued that Paine was a direct influence on the writing of this document.
But if we are to speak more broadly, the idea of natural rights goes back to previous Enlightenment thinkers such as John Locke. And natural rights originates from natural law, an idea Christians inherited from Stoics. There were lots of ideas that had been floating around for a while.
LikeLike
I think you’d really prefer him not to be a liberal who can see some of the lefts tirades on society are unfairly fought. I think he’s proven that his approach won’t be one of ideology-driven critique of society as a whole and that the many positives he speaks to have meaning and connection to our world. To ignore the positives at your own peril.
I guess I see your response as highlighting a different interpretation not actually invalidating any of his argument.
LikeLike
Re Graph 5 — Measuring Genuine Progress — Pinker’s ideas (and apparently yours too, since you miss it) about GDP or even GPI as meaningful measures of progress are utterly wrongheaded. Why? These are measures of >average< economic progress across an entire economy. But when you consider the large and increasing economic inequity, you realize that the gains they portray are almost entirely at the top — relatively few wealthy people.
This is a huge misconception committed not only by the Right, but even by so-called liberals like Krugman.
Here's an article that calls these "plutocratic measures of economic growth", and illustrates it nicely.
https://ftalphaville.ft.com/2018/07/26/1532583000000/What-s-the-matter-with-GDP-/
LikeLiked by 1 person
I find no consolation in GPI vs. GDP, though I wouldn’t want to be put in the position to defend GDP. But one thing I found somewhat humorous is the idea that if GPI is a better measurement, and GPI is falling in tandem with racist, sexist, and homophobic jokes, maybe that means we ought to be making more of those.
Here is my go-to example of why people arguing that things aren’t better after the enlightenment or capitalism appear to be wrong. A homeless person today can collapse from a heart attack in front of a hospital and in relatively short order undergo quadruple bypass surgery and live. J. D. Rockefeller would’ve just died, no matter how rich he was. Technological advancement, not only in medicine, but in all the other realms, in many ways defines the progress we’ve seen, and technological advancement as we’ve seen from the hockey stick moment in the 20th century, is better cultivated in an enlightenment capitalist environment. China struggles to innovate, so they routinely copy other countries. And where they do innovate, those companies adhere to capitalism (thus making capitalism the great evil of the East until it makes the government money). The religious authoritarian Middle East struggles to innovate and usually winds up with hand-me-downs from the West.
The dirty little secret to human progress is innovation, and in terms of cultivating innovation, any argument positing that capitalism is the same as or worse than any other known economic model is frankly history-blind. It’s really quite simple. We as humans feel a great desire to solve problems for two entities: Ourselves (I’ll include our family under this umbrella), and our society. Wouldn’t it be great if one could solve problems for both at the same time? That is essentially what capitalism attempts, and although not perfect, does a much better job than any model that, if not completely committed to society, is at least mostly committed to society (i.e. Marxism, Communism, Socialism). The argument could be made that under something like communism, any effort to benefit society inadvertently benefits oneself, but recognize the key difference here. Capitalism is modeled this way: “Help yourself, and then inadvertently help society.” Communism is modeled this way: “Help society, and then inadvertently help yourself.” Which one are you going to work harder at? The one where your effort predicts how well you do first, then how well society does later, or the model where your effort predicts how well society does first, then you later?
Before I say anything else, it’s important to frame this around the creature we are. If I were writing this to a planet of sentient ants, I would not be writing the same thing. But I’m writing this in an environment of homo sapiens. We have a very strong, very complex, sometimes very clunky but often quite tuned social hierarchical system which emphasizes individual independent behavior in harmony with collective behavior. I would correlate this lightly with the fact that all of us have that little daemon in our head, whispering sweet nothings to us, narrating every facet of our lives, which we casually refer to as the “self”. No other animal, from what we can tell, has that same inner dialogue. No other animal, as far as we can tell, even seems to have a concept of “self”. And I correlate these two things because a little voice that you identify with suggesting to exhibit certain behaviors that you presumably care to listen to and might even bother to protect means that you’ll at least be a little more selfish than a creature without such a voice. Bees, for example, will gladly give their lives for the hive and sting their stingers into intruders without hesitation, knowing (I guess “knowing”) what they did means certain death. When humans do that, we call that an anomaly and give out medals and write heroic stories about them. The other bees don’t care if some bees gave their lives because that’s expected. You’re a bee, you’re supposed to do that. In the human case, you sit around and think “wow, that was incredible what that other guy did, some people are really amazing. I know I couldn’t do it. I’d be too scared.” And for that too I’d say you’re a human, you’re supposed to do that.
I’d even go as far to say that as long as selfishness exists, capitalism is the preferred economic model to achieve human growth. As far back as you want to go, the number one indicator of increases in wealth, healthcare, and overall education, is an increase in innovation. And innovation, framed around this selfish species, from what we can tell thus far works best in a Steven Pinker capitalist technocratic nightmare.
LikeLike
The discussion about the Elephant Graph conceals the most important fact, that is the improvement of absolute poverty, which is the most important issue; the rise of incarceration doesn’t count the fact that it lead to a reduction of crime and that conditions in jail have dramatically improved; the hint about racial disparity in incarceration omits all the other about racism (like aggression and discrimination), which have increased too.
“brave individuals who had to resist the opprobrium of the Steven Pinkers”
Now even Steven Pinker, with his openly progressive stances, has become a racist and a segregationist against which progressive should fight. This article is the perfect example of what regressive left means.
LikeLike
Hi f.dd.91,
What do you mean by “the hint about racial disparity in incarceration omits all the other about racism (like aggression and discrimination), which have increased too.”
All the other what?
LikeLike